Sacks Spiral

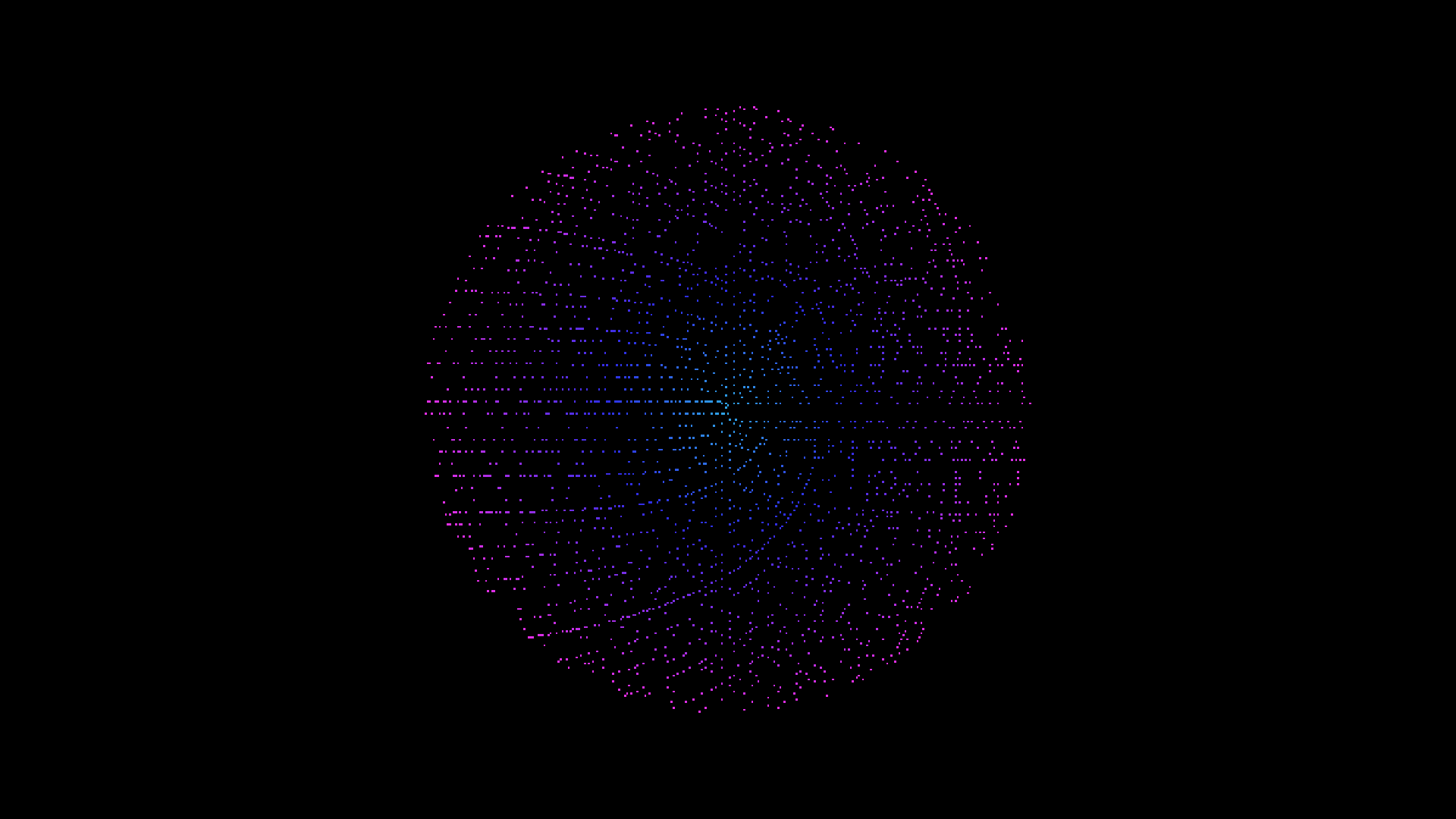
The Sacks and Ulams spiral explores prime numbers, by displaying them in a regular, observable pattern. The Sacks spiral works by looping integers, and detecting prime numbers as they occur. Should the number be detected as a prime number, a coloured dot is displayed in the corresponding numerical position within the spiral. If the number is not detected as a a prime, a dot is not shown. The dots are subsequently coloured according to how large the number is, thus a spiral is created.

The Ulams spiral is similar to the Sacks spiral, but instead of looping in a spiral effect, detected primes are looped in a square, thus creating a different pattern of prime numbers.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
Module SacksSpiral
    ' Equations
    '  x = -cos(sqrt(i)*2*pi)*sqrt(i)
    '  y = sin(sqrt(i)*2*pi)*sqrt(i) 

    Sub Main()
        Dim i As Integer = 0
        Using BMP As New Drawing.Bitmap(301, 301)
            Dim x As Integer = 0
            Dim y As Integer = 0

            Primes.Primes(22726)

            For i = 0 To Primes.TruePrimesList.Count - 1
                ' Next coordinates
                x = -1 * Math.Cos(Math.Sqrt(Primes.TruePrimesList(i)) * 2 * Math.PI) * Math.Sqrt(Primes.TruePrimesList(i)) + 150
                y = Math.Sin(Math.Sqrt(Primes.TruePrimesList(i)) * 2 * Math.PI) * Math.Sqrt(Primes.TruePrimesList(i)) + 150

                ' Colour hue is based on square root of number
                Dim Colour As New HSBColour(0.663328938 * Math.Sqrt(Primes.TruePrimesList(i)) + 200, 0.8, 0.9)

                BMP.SetPixel(x, y, Colour.HSBToRGB)
            Next
            BMP.Save("SacksSpiral.bmp", Drawing.Imaging.ImageFormat.Bmp)
            Console.WriteLine("Finished")
            Console.ReadLine()
        End Using
    End Sub
End Module

Module Primes
    Public Property PrimesFactorList As New System.Collections.Generic.List(Of Integer) 'Store Primes up to Square Root of 'n'
    Public Property TruePrimesList As New System.Collections.Generic.List(Of Integer) ' The list of combined primes
    ' Determine if Number is Prime
    Public Sub IsPrime(inputnum)
        For i = 3 To Math.Sqrt(inputnum) Step 2
            If inputnum Mod i = 0 Then
                Exit Sub
            End If
        Next
        PrimesFactorList.Add(inputnum)
    End Sub

    Sub Primes(Number As Integer)
        Console.WriteLine("Primes")
        Console.WriteLine("Parameter: n - " & Number)

        Dim PrimesFactorThread As New System.Collections.Generic.List(Of System.Threading.Thread) ' Stores All Threads Crated
        PrimesFactorList.Add(2) ' Add the Prime Number 2

        For i = 3 To Math.Sqrt(Number) Step 2 ' Find all primes up to square root of number
            Dim Num As Integer = i
            Dim td As New System.Threading.Thread(Sub() IsPrime(Num)) ' Start Thread of IsPrimes - Determine if Num is Prime Number
            td.Start()
            PrimesFactorThread.Add(td) ' Add Thread to Collection of Threads
        Next

        ' Wait for all threads to finish
        For Each item As Threading.Thread In PrimesFactorThread
            Do Until item.IsAlive = False
            Loop
        Next

        PrimesFactorThread.Clear()
        PrimesFactorThread = Nothing

        Dim PrimesArray(Number - 2) As Boolean ' Sieve - Starts off False
        For Each item As Integer In PrimesFactorList ' Loop through Factors
            For i = 1 To Number / item ' Loop until the last multiple before 'Number'
                PrimesArray(i * item - 2) = True ' Eliminate Numbers using Multiples (Sieve)
            Next
        Next

        TruePrimesList.AddRange(PrimesFactorList) ' Add the primes from PrimesFactorList (Primes up to the square root of Number)
        PrimesFactorList.Clear()

        For i = 0 To PrimesArray.Length - 1 ' Loop through PrimesArray
            If PrimesArray(i) = False Then ' If Index is still false, then that means that it's prime
                TruePrimesList.Add(i + 2)
            End If
        Next

        PrimesArray = Nothing
        TruePrimesList.Sort() ' Sort the List

        Console.WriteLine("Number of Primes: " & TruePrimesList.Count & Environment.NewLine) ' Output
        GC.Collect()
    End Sub
End Module

References

https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes http://www.dcs.gla.ac.uk/~jhw/spirals/